How to Determine Which Graph Is Best Graph Theory
If G is not a null graph then χ G 2. Applying this theorem we note that the original degree sequence is graphical if and only if the degree sequence given by 7 7 7 5 4 3 3 2 1 is graphical.
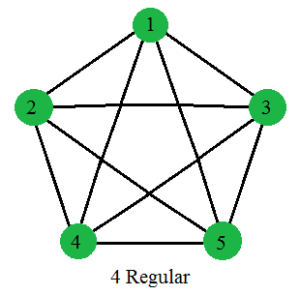
Regular Graph In Graph Theory Geeksforgeeks
Thus the oriented graph obtained in this way is a digraph.
. In an unweighted directed graph G every pair of vertices u and v should. Can you draw a K_5 a K_6. Graph Databases for Beginners.
All the edges from the edge set have one endpoint vertex from the set and another endpoint vertex from the set. A graph with n vertices where every two vertices are connected to each other is called a fully connected graph. For any graph G κG λG δG where δG is the minimum degree of any vertex in G Mengers theorem A graph G is k-connected if and only if any pair of vertices in G are linked by at least k independent paths Mengers theorem A graph G is k-edge-connected if and only if any pair of vertices in G are.
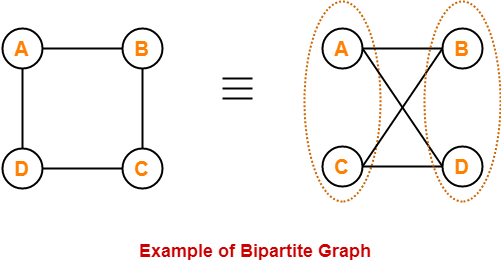
If no permutation was a cycle the graph is not Hamiltonian. The vertex set of can be partitioned into two disjoint and independent sets and. Take a look at the following graph For the graph shown above Euler path exists false Euler circuit exists false Hamiltonian cycle exists true Hamiltonian path exists true G has four vertices with odd degree hence it is not traversable.
It can help you to find the one who spread the wrong rumor in a classroom to a mastermind of a serious crime. However team B was beaten by team D and beat team A. Except for total and complete nerds a lot of people didnt like mathematics while growing up.
Assume G is the adjacency matrix for your graph. Theres a common one-liner I hate mathbut I love counting money. In K_n how many edges are there.
The second half of the book is on graph theory and reminds me of the Trudeau book but with more technical explanations eg you get into the matrix calculations. By skipping the internal edges the graph has a Hamiltonian cycle passing through all the vertices. Network Flows Ahuja Magnanti and Orlin.
Make laplacian matrix via subtraction. Graph theory is the study of relationship between the vertices nodes and edges lines. Graph Theory Predictive Modeling.
Build D which is a diagonal matrix with the same size as G put degree of Nth node in the Nth diagonal element. Third but the most most important Application of graph theory in day-to-day life. If the smallest eigenvalue is strictly bigger then zero or the same as if zero is not an eigenvelue then it is connected.
As you known graph theory is all about linking and the study of linking. χ G 1 if and only if G is a null graph. We can keep on reiterating to get the following degree lists.
To answer the question. L D - G. Try every permutation of vertices and if one of the permutations is a cycle then the graph is Hamiltonian.
Now in graph weve two partitioned vertex sets and Suppose weve an edge. Connect and share knowledge within a single location that is structured and easy to search. Given an unweighted directed graph G as a path matrix the task is to find out if the graph is Strongly Connected or Unilaterally Connected or Weakly Connected.
Graph theory is the study of objects and the relationships between them. Lets try to simplify it further. Simply put no two vertices of an edge should be of the same color.
In fact of all school subjects its the most consistently derided in pop culture which is the. Chromatic Number The minimum number of colors required for vertex coloring of graph G is called as the chromatic number of G denoted by X G. In an attempt to determine the dominant vertices in a tournament mathematical sociologist H.
We proceed with the HavelHakimi Theorem which determines whether a degree sequence can represent a simple graph. Given a set of nodes connections which can abstract anything from city layouts to computer data graph theory provides a helpful tool to quantify simplify the many moving parts of dynamic systems. If the graph contains a bridge an edge which disconnects the graph then clearly no such orientation exists.
In the following a general algorithm to construct undirected graphs from a given atoms object is presented. You cannot convince your friends that the graph is non-Hamiltonian without trying all permutations. If so you get a certificate.
Formally a graph is denoted as a pair G V E. The graph theory form of the initial problem is to determine for which graphs there is an orientation which makes the resulting digraph diconnected. In Mathematics it is a sub-field that deals with the study of graphs.
Documentation hereSage has knowledge of graph theory. Determine whether a graph is connected or disconnected Find the shortest path through a graph using Dijkstras Algorithm In this lesson we will introduce Graph Theory a field of mathematics that started approximately 300 years ago to help solve problems such as finding the shortest path between two locations. Look at the graph laplacian D-A where D is the diagonal matrix with corresponding degrees of vertices on the diagonal.
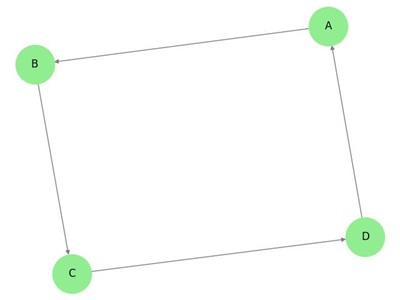
Lets consider a graph The graph is a bipartite graph if. Although interesting its probably best suited for those that really want to dive into the math theory. Unclear which team is the best As the figure suggests team A and team D both won two games.
It is a pictorial representation that represents the Mathematical truth. FBI investigations years ago a graph was created that includes the terrorists. Studying graphs through a framework provides answers to many arrangement networking optimization matching and operational problems.
6 6 4 3 2 2 1 0. You might consider signing up for a free Sagemath Cloud account which gives you the power of the computer algebra system Sage along with the sagetex package in LaTeX. For example named graphs graph parameters and even LaTeX optionsThat means you can create your graphs using tikz or use.
Graph Theory is the study of points and lines. Also called a K_n everyones friends in fact best friends 12. How many k-cliques are there in K_n.
A graph is said to be strongly connected if every pair of vertices u v in the graph contains a path between each other.
Graph Types And Applications Geeksforgeeks

Complete Graph Definition Example Video Lesson Transcript Study Com

Complete Graph Definition Example Video Lesson Transcript Study Com

Connected Graph Vs Complete Graph Video Lesson Transcript Study Com
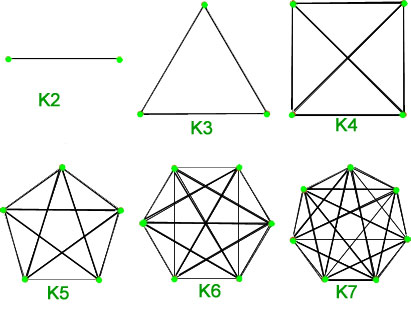
Mathematics Graph Theory Basics Set 2 Geeksforgeeks

Connected Graph Vs Complete Graph Video Lesson Transcript Study Com

Complete Graph Definition Example Video Lesson Transcript Study Com
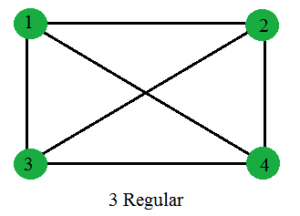
Regular Graph In Graph Theory Geeksforgeeks
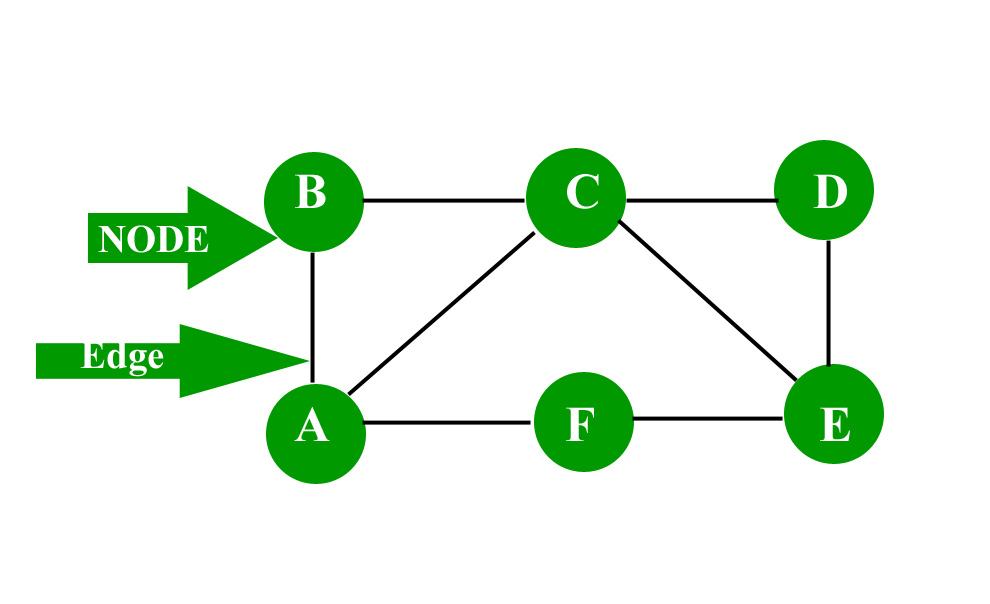
Graph Measurements Length Distance Diameter Eccentricity Radius Center Geeksforgeeks
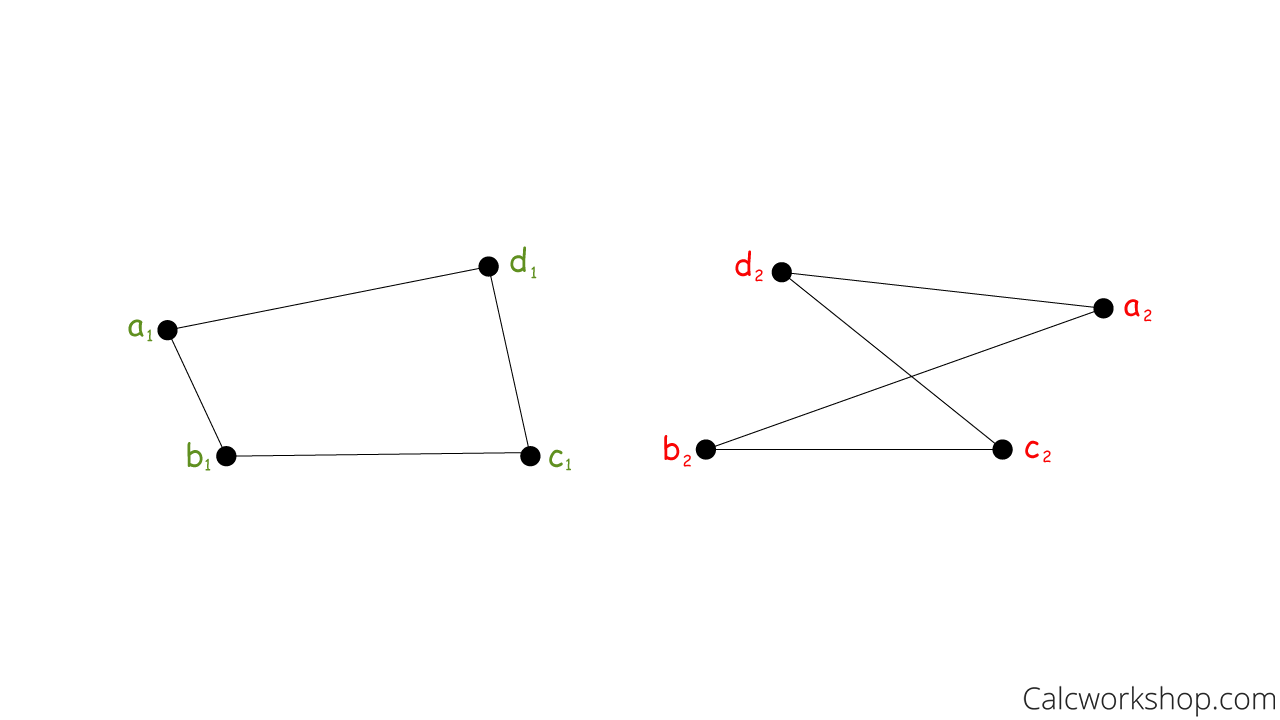
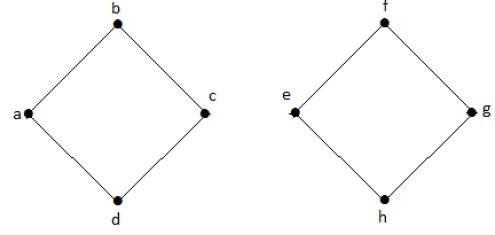
Isomorphic Graph Explained W 15 Worked Examples
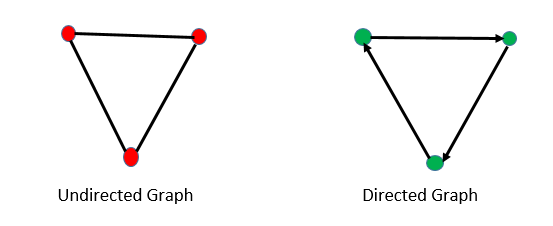
Graph Theory Discrete Mathematics Types Of Graphs

Bipartite Graph Bipartite Graph Example Properties Gate Vidyalay
Comments
Post a Comment